What is the smallest interesting colour code? The first possible answer is the 7 qubit Steane code. Except, it isn’t especially interesting. In particular, the transversal gates of the Steane code are the Clifford group. Really interesting codes have transversal gates outside the Clifford group, and may be used in concert with gauge-fixing or magic state distillation.

Those familiar with the field will immediately retort that the 15 qubit Reed-Muller code is a colour code as was observed in 2006 by Bombin and Martin-Delgado. And it is interesting. The non-Clifford gate

is transversal for the 15 qubit code, in the sense that
.
However, there is a smaller colour code with only 8 physical qubits that is also interesting. Though the smaller code is a different flavour of interesting. The logical non-Clifford is a CCZ (control-control-Z), which is Clifford equivalent to a Toffoli.

Here, I want to describe this colour code and tell you about some intriguing connections to the topics of gate-synthesis and magic state distillation. Indeed, I discovered this curious code in the context of magic states, and it enables us to distill 8 noisy T-states into a less noisy CCZ magic state. This distillation protocol is essentially a different perspective on the results of Cody Jones and Bryan Eastin. Later, me and Mark Howard extended the construction to all gates in the third level of the Clifford hierarchy (see either the short paper or long paper). But I had an algebraic description of the code and I never noticed the code had a neat geometric representation as a colour code, which can be extended to higher distance colour codes (more on this later). Rather, at the FTQT Benasque meeting I was talking to Dan Browne and he described this colour code to me, and only then did I realise it was the same code I’d been working with. So I thank Dan for allowing me to steal his insight and turn it into a blog post.

Onwards, to the description of the smallest interesting colour code. It is a [[8,3,2]] code. Translation: it uses 8 physical qubits to encode 3 logical qubits and has distance 2 (it can detect any one error, but not correct it). The geometric description of the rests upon a single cubic cell with 8 vertices, each corresponding to a qubit as follows:

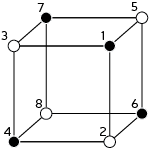
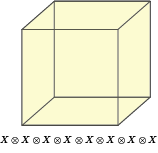
Note the numerical labels of qubits, which relate to the order of operators in tensor products used below. Also, I have two-coloured the vertices into black/white vertices, where black vertices are only adjacent to white vertices. The two-colorability of vertices is known to be directly related to the other colorability properties of colour codes (my preferred proof of this relation is Lemma 3 of [self-promoting link] ). Here, the relevance of two-colorability is that our transversal gate is achieved by applying to black vertices and to white vertices, so that

Notice that the logical CCZ involves the three logical qubits (labeled L1, L2, L3) of a single block of the 8 qubit code.

Now, lets define the code so we can verify these claims.

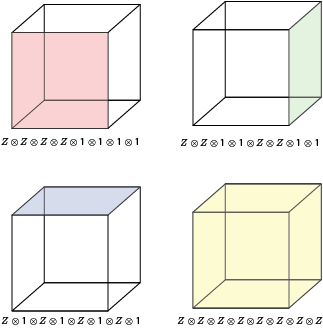
The Z stabilisers of the code corresponds to the face and cell operators of the cube. Only 3 face operators are needed to generate the stabiliser group. Other face operators emerge from group closure.

The sole X stabiliser of the code corresponds to the cell operators of the cube.

It is easy to check these all commute.

The logical X operators are membranes spanning the lattice. Yet, the lattice is a single unit cell and so a membrane is simply a face. The logical Z operators are strings spanning the lattice, and so are edges of this unit cell.

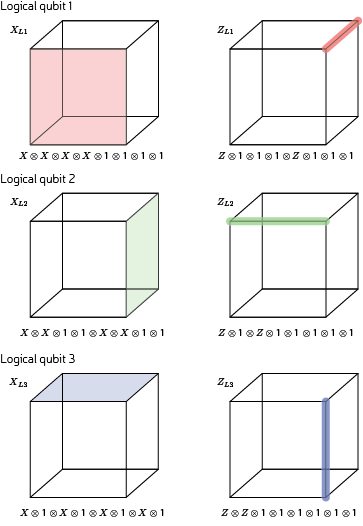
Again the relevant commutation and anti-commutation relations are easy to see in this geometric picture.

Having defined the code, there are many different ways to verify the transversality properties. Most mundanely, one can simply write out the computational basis states

… exercise to reader to fill in these states …

and then check the transversality properties. For qubits in the state, simply add a phase to black (even labelled) and a phase for white (odd labelled) qubits. And out pops the CCZ gate.

The above calculation may not yield a great deal of intuition on the origin of CCZ transversality. A deeper understanding is reached by learning about a generalised notion of triorthogonal codes. Bravyi and Haah gave the original conception of triorthogonal codes to construct codes where the transversal gate is a logical . In our synthillation paper, we showed that this notion can be generalised to explain transversality of all gates in the Clifford hierarchy. While this proof encompasses CCZ gates, the proof’s generality may obscure the applicability to the above colour code. So let me paraphrase the argument for this special case (and slightly modify for a colored lattice). To get a CCZ logical we need:

1. All the X logical operators have support on an equal number of black and white vertices;
2. For any pair of X logical operators, the common support contains an equal number of black and white vertices;
3. For any trio of X logical operators, the common support contains an unequal number of black and white vertices, with the difference between an odd number;

One can easily check these conditions are satisfied on the cube unit cell. There are some additional demands on the X stabilisers, but these are very similar to the demands for transversality of a T-gate.

I also promised a connection to gate-synthesis, and this will explain why the code has 8 qubits! There are various papers (e.g. Amy and Mosca) that explain how to unitarily compose T gates with CNOT gates to implement any gate in the 3rd level of the Clifford hierarchy. For the CCZ gate, it is well known that 7 T-gates are optimal (at least without using any special tricks). Furthermore, this can be implemented in T-depth one (all 7 T gate are performed simultaneously) provided we use some ancillary qubits (first shown by Selinger). The CNOT gates preceding the T gates can be interpreted as an encoding unitary into some quantum code. However, the codes used by optimal gate-synthesis have no X-stabilisers, and so are distance one. The strategy me and Mark pursued was to take this trivial code and pad it out with extra qubits and extra stabilisers without harming its transversality properties. It transpires that for a circuit composed of solely CCZ gates (possibly very many CCZ gates), this padding is possible using only 1 additional qubit. Therefore, there is an error protected code using only one more qubit than optimal unitary gate-synthesis. 7+1=8, which explains the relation between the 8 qubit code and CCZ (which requires 7 T-gates). This post is skimming many details, but hopefully conveys a taste of the underlying mathematics. The full gory details appear in Example IV.1 of our paper.

Earlier in the post, I also alluded to higher distance colour codes. Here I was referring to unfolding the colour code by Kubica, Yoshida and Pastawski. This is a neat paper on the correspondence between colour codes and surface codes. However, buried within the paper is the observation that 3D colour codes (of large distance) can have CCZ transversality of the above nature. An important point is that the bulk lattice of a 3D colour code must be 4-valent, and this can only be violated at boundaries and defects. Therefore, these larger colour codes are not cubic lattices (which would be 6-valent in the bulk). However, the boundary conditions have some geometry and Kubica and company fix these boundaries to be cubic. Hence, we see that the smallest interesting colour code corresponds is an instance of this family of codes where the set of bulk qubits is empty. All qubits sit on the boundary.

This covers everything I wanted to say here. It has been a longer and more technical post than usual. But I think the connections between these different topics and papers is interesting and worth pointing out.